자료 구조 정리

선형 자료구조

요소가 일렬로 나열되어 있는 자료구조

1. 연결 리스트 (LinkedList)

• 데이터 요소를 연결된 노드로 표현하는 방식
• LinkedList는 동적으로 크기가 조절될 수 있으며, 데이터의 삽입과 삭제가 빠르게 이루어짐

▫️노드(Node) : LinkedList의 기본 구성 요소로, 데이터와 다음 노드를 가리키는 링크(포인터)로 구성된다.
▫️헤드(Head) : LinkedList의 첫 번째 노드를 가리키는 포인터입니다. LinkedList에서 데이터에 접근하기 위해서는 헤드부터 시작해야 한다.
▫️데이터(Data) : 각 노드가 저장하는 실제 값 또는 객체이다.
▫️링크(포인터/Pointer) : 노드들을 연결하는 역할을 한다. 각 노드는 다음 노드를 가리키는 링크를 가지고 있다. 

▫️싱글 연결 리스트 : next 포인터만 가진다
▫️이중 연결 리스트 : next 포인터와 prev 포인터를 가진다
▫️원형 이중 연결 리스트 : 이중 연결 리스트와 같지만 마지막 노드의 next 포인터가 헤드 노드를 가리킨다 

class Node {
    int data; // 데이터를 저장하는 변수
    Node next; // 다음 노드를 가리키는 링크(포인터)

    public Node(int data) {
        this.data = data;
        this.next = null; // 초기에는 다음 노드를 가리키는 링크가 없으므로 null로 설정
    }
}

class LinkedList {
    Node head; // 첫 번째 노드를 가리키는 헤드(포인터)

    public LinkedList() {
        this.head = null; // 초기에는 헤드가 null인 빈 LinkedList
    }

    // 노드를 LinkedList의 맨 끝에 추가하는 메서드
    public void append(int data) {
        Node newNode = new Node(data); // 새로운 노드 생성

        if (head == null) {
            // LinkedList가 비어있는 경우, 헤드로 설정
            head = newNode;
        } else {
            Node current = head;
            while (current.next != null) {
                current = current.next; // 마지막 노드까지 이동
            }
            current.next = newNode; // 마지막 노드의 다음 링크에 새로운 노드를 연결
        }
    }

    // LinkedList의 모든 요소를 출력하는 메서드
    public void display() {
        Node current = head;
        while (current != null) {
            System.out.print(current.data + " "); // 현재 노드의 데이터 출력
            current = current.next; // 다음 노드로 이동
        }
        System.out.println();
    }
}

public class Main {
    public static void main(String[] args) {
        LinkedList list = new LinkedList(); // LinkedList 인스턴스 생성

        list.append(1); // LinkedList에 1을 추가
        list.append(2); // LinkedList에 2를 추가
        list.append(3); // LinkedList에 3을 추가

        list.display(); // LinkedList의 모든 요소를 출력 (1 2 3)
    }
}

2. 배열(Array)

▫️같은 타입의 변수들로 이루어져 있음
▫️크기가 정해져 있음
▫️인접한 메모리 위치에 있는 데이터를 모아놓은 집합
▫️중복을 허용하고 순서가 있음
▫️정적 배열
▫️인덱스에 빠르게 접근할 수 있음
▫️삽입/삭제가 비효율적 → 중간에 값을 넣거나 빼려면 값을 하나씩 밀거나 당겨야 함 

 

	랜덤 접근 (Random Access)	순차적 접근 (Sequential Access)
정의	원하는 위치의 데이터를 바로 읽거나 쓸 수 있는 방식	처음부터 차례대로 데이터를 읽거나 써야 하는 방식
속도	빠름 (O(1), 위치만 알면 즉시 접근)	느릴 수 있음 (O(n), 처음부터 찾아야 함)
예시	배열(Array)	연결 리스트(LinkedList), 테이프

랜덤 접근(Random Access)

• 배열처럼 인덱스 번호만 알면 그 위치의 데이터에 바로 접근할 수 있다 .
• 데이터가 연속된 메모리 공간에 있기 때문에 가능.

📌 예: 배열

int[] arr = {10, 20, 30, 40, 50};

System.out.println(arr[2]);  // 30 출력

그래서 배열은 검색, 읽기 속도가 매우 빠름

순차적 접근(Sequential Access)

• 데이터를 찾으려면 처음부터 차례차례 따라가야 함.
• 데이터들이 연결되어 있고, 하나하나 방문하지 않으면 다음 걸 알 수 없음.

📌 예: 연결 리스트

head → [10] → [20] → [30] → [40]

찾고 싶은 값: 30
→ 10부터 시작해서 하나하나 따라가야 30에 도착할 수 있음

• LinkedList는 arr[2] 같은 직접 접근이 안 됨.
• 무조건 처음부터 next를 따라가야 하기 때문에 시간이 더 걸림.

데이터를 자주 조회할 때	배열 (랜덤 접근이 빠르니까)
데이터를 자주 추가/삭제할 때	연결 리스트 (구조 변경이 쉬움)

3. 벡터(Vector)

▫️동적 배열(Dynamic Array) → 크기를 자동으로 조절할 수 있는 배열
▫️컴파일 시점에 개수를 모른다면 벡터를 써야 함
▫️인덱스를 이용한 랜덤 접근 가능
▫️ArrayList와 매우 비슷하지만, 동기화(synchronization) 기능이 있어 멀티스레드 환경에서 안전
▫️자동 확장 → 내부적으로 크기를 2배씩 늘림 

import java.util.Vector;

public class Main {
    public static void main(String[] args) {
        Vector<String> vec = new Vector<>();

        vec.add("사과");
        vec.add("바나나");
        vec.add("체리");

        System.out.println("전체 과일: " + vec);
        System.out.println("두 번째 과일: " + vec.get(1));  // 인덱스 1
    }
}

전체 과일: [사과, 바나나, 체리]
두 번째 과일: 바나나

주요 메서드

add(value)	값 추가
get(index)	인덱스 위치의 값 가져오기
set(index, value)	특정 위치 값 수정
remove(index)	인덱스 위치 값 제거
size()	요소 개수 확인
clear()	전체 요소 삭제

내부 동작

• Vector는 내부적으로 배열을 사용함.
• 요소를 계속 추가하면, 공간이 부족할 때 기존 배열보다 2배 큰 배열을 새로 만들어 복사해서 사용 </aside>
• Vector vs ArrayList

	Vector	ArrayList
동기화	✅ (멀티스레드 안전)	❌ (빠르지만 멀티스레드에는 비안전)
성능	느림 (동기화 오버헤드)	빠름
용도	멀티스레드 환경	단일 스레드 환경

대부분의 경우는 ArrayList를 사용하고, 멀티스레드 환경에서만 Vector를 고려.

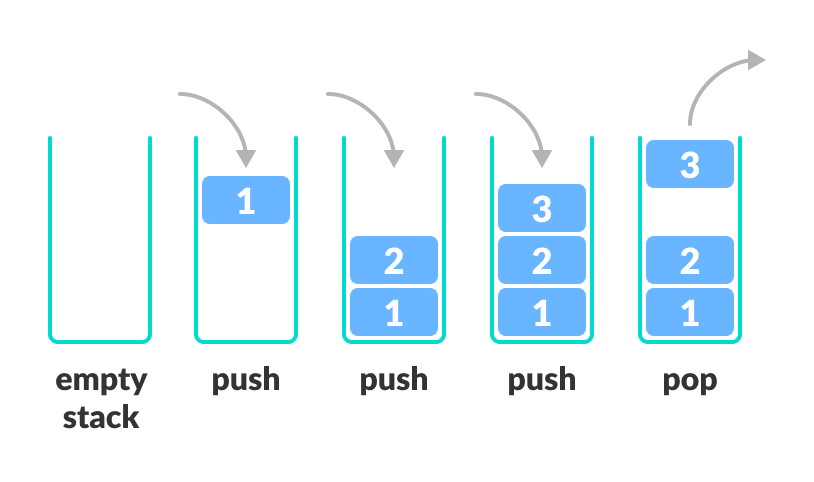
4. 스택(Stack)

• 마지막에 들어간 데이터가 가장 첫번째로 나옴
• LIFO (Last In, First Out)

주요 연산

push()	데이터 추가 (맨 위에 쌓음)
pop()	데이터 제거 (맨 위에서 꺼냄)
peek()	가장 위의 데이터 확인 (제거 X)
isEmpty()	비었는지 확인

import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();

        stack.push(10);
        stack.push(20);
        stack.push(30);

        System.out.println(stack.pop());  // 30
        System.out.println(stack.peek()); // 20
        System.out.println(stack.isEmpty()); // false
    }
}

5. 큐(Queue)

• 먼저 들어간 데이터가 먼저 나온다
• FIFO (First In, First Out)

주요 연산

offer()	데이터 추가 (뒤에 넣음)
poll()	데이터 제거 (앞에서 꺼냄)
peek()	앞의 데이터 확인 (제거 X)
isEmpty()	비었는지 확인

import java.util.LinkedList;
import java.util.Queue;

public class Main {
    public static void main(String[] args) {
        Queue<String> queue = new LinkedList<>();

        queue.offer("A");
        queue.offer("B");
        queue.offer("C");

        System.out.println(queue.poll());  // A
        System.out.println(queue.peek());  // B
        System.out.println(queue.isEmpty()); // false
    }
}

 

스택	웹 브라우저 "뒤로가기", 계산기 괄호 검사, 재귀 함수 호출
큐	은행 번호표, 프린터 대기열, BFS 알고리즘, OS 스케줄링

---

비선형 자료구조

일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조

1. 그래프

정점(Node, Vertex)과 간선(Edge)으로 구성된 자료구조

• 간선(Edge)에 방향이 있는 그래프
• 한 노드에서 다른 노드로 일방적으로 연결됨

단방향(Directed)

A → B
↓
C

양방향(Undirected)

• 간선이 양쪽 방향으로 연결됨
• A에서 B로 갈 수 있으면, B에서도 A로 갈 수 있음

A — B
|    |
C — D

가중치(Weight)

그래프에서 간선(Edge)마다 붙는 숫자 값

A ——10—— B
|         |
5         2
|         |
C ——1 —— D

• 간선의 가중치:

A–B: 10km
A–C: 5km
C–D: 1km
B–D: 2km

여기서 가중치는 "거리"

2. 트리(Tree)

사이클(순환)이 없는 계층적 구조의 그래프

트리의 특징

• 부모-자식의 구조를 가짐
• V-1 = E 라는 특징이 있음 간선수는 노드 수 -1
• 임의의 두 노드의 사이의 경로는 ‘유일무이’ 하게 존재→ 트리 내의 어떤 노드와 어떤 노드가지의 경로는 반드시 있음

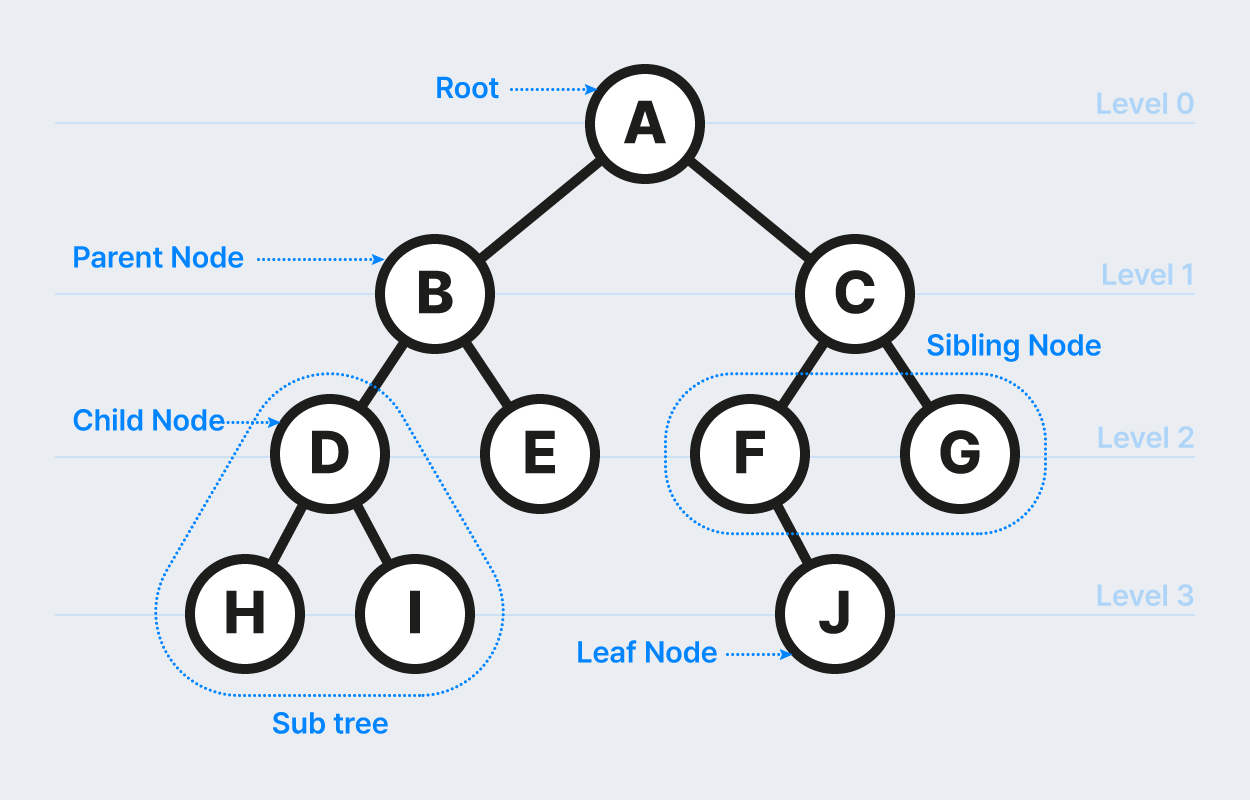
노드(Node)	데이터를 담는 하나의 점 (예: 숫자, 문자 등)
루트(Root)	트리의 맨 위에 있는 노드 (출발점)
간선(Edge)	노드와 노드를 연결하는 선
자식(Child)	어떤 노드의 아래쪽에 연결된 노드
부모(Parent)	자식 노드를 가진 노드
리프(Leaf)	자식이 없는 노드
서브트리(Subtree)	전체 트리의 일부 (자식 포함된 구조)

        A         ← 루트 (레벨 0)
       / \\
      B   C       ← 레벨 1
     / \\   \\
    D   E   F     ← 레벨 2

 

용어	정의	예시 (위 트리에서 A 기준)
레벨	루트에서 얼마나 떨어졌는지	A: 0, B: 1, D: 2
깊이	루트에서 해당 노드까지 간선 수	D: 2
높이	노드에서 가장 깊은 자식까지 거리	A의 높이: 2, D의 높이: 0

이진 트리 (Binary Tree)

모든 노드가 최대 두 개의 자식 노드를 가지는 트리

이진 탐색 트리 (Binary Search Tree, BST)

왼쪽 자식 < 부모 < 오른쪽 자식이라는 조건을 가지는 이진 트리

      8
     / \\
    3   10
   / \\    \\
  1   6    14

• 정렬된 구조 → 탐색에 유리
• 탐색 성능
  • 최선: O(log n)
  • 최악: O(n) → 한쪽으로 치우치면 성능 저하

3. 힙 트리 (Heap Tree)

• 완전 이진 트리 기반의 트리 구조 부모 노드와 자식 노드 간의 우선순위(값) 조건을 만족
• 항상 루트가 가장 우선순위 높은 값
• 삽입/삭제 시 O(log n)
• 우선순위 큐(Priority Queue) 구현에 사용

최소 힙 (Min Heap)	부모 ≤ 자식 → 루트가 최소값
최대 힙 (Max Heap)	부모 ≥ 자식 → 루트가 최대값

1. 최대 힙에 삽입 (Insert)

📌 과정

1. 맨 끝에 새 노드 추가 (완전 이진 트리 유지)
2. 위로 올라가며 부모와 비교
3. 부모보다 크면 교환(Swap) → 이 과정을 반복 (Heapify-Up)

예제: 50, 30, 40, 10, 20, 35 → 삽입(60)

1) 맨 뒤에 삽입

       50
      /  \\
    30    40
   / \\   / \\
 10 20 35 60 ← 새 노드

2) 부모(40)보다 크니까 스왑

       50
      /  \\
    30    60
   / \\   / \\
 10 20 35 40

3) 다시 부모(50)보다 크니까 스왑

       60
      /  \\
    30    50
   / \\   / \\
 10 20 35 40

✨ 완료!

👉 삽입 시간 복잡도: O(log n) (트리 높이만큼 올라감)

2. 최대 힙에서 삭제 (Remove Max)

📌 과정

1. 루트(최댓값)를 제거
2. 마지막 노드를 루트에 위치시킴
3. 아래로 내려가며 큰 자식과 교환 (Heapify-Down)

예제: 위 상태에서 삭제() (최댓값 60 제거)

1) 마지막 노드(40)를 루트로 이동

       40
      /  \\
    30    50
   / \\   /
 10 20 35

2) 자식 중 큰 값(50)과 스왑

       50
      /  \\
    30    40
   / \\   /
 10 20 35

✨ 완료!

👉 삭제 시간 복잡도: O(log n) (트리 높이만큼 내려감)

4. 우선순위 큐(Priority Queue)

순서대로 나오는 큐가 아니라, 중요한(우선순위가 높은) 것부터 나오는 큐

자바에서의 PriorityQueue

import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        PriorityQueue<Integer> pq = new PriorityQueue<>(); // 기본: 최소 힙

        pq.add(5);
        pq.add(1);
        pq.add(3);

        while (!pq.isEmpty()) {
            System.out.println(pq.poll()); // 작은 값부터 출력: 1, 3, 5
        }
    }
}

최대 힙으로 만들기 (우선순위 큰 게 먼저)

기본PriorityQueue는 최소 힙(작은 값 우선)이므로

최대 힙처럼 쓰고 싶다면 Collections.reverseOrder()사용

PriorityQueue<Integer> maxPQ = new PriorityQueue<>(Collections.reverseOrder());

maxPQ.add(5);
maxPQ.add(1);
maxPQ.add(3);

while (!maxPQ.isEmpty()) {
    System.out.println(maxPQ.poll()); // 큰 값부터 출력: 5, 3, 1
}

5. Map (맵)

• 데이터를 키(key) – 값(value) 쌍으로 저장하는 자료구조
• 키를 통해 값을 빠르게 찾을 수 있다

Map<String, Integer> map = new HashMap<>();
map.put("apple", 3);
map.put("banana", 5);

System.out.println(map.get("banana")); // 출력: 5

• key는 중복 ❌, value는 중복 가능
• get(key)으로 값 조회
• 구현체: HashMap, TreeMap, LinkedHashMap, Hashtable 등

6. Set (셋)

• 중복 없는 값만 저장하는 자료구조
• 순서는 중요하지 않음

Set<String> set = new HashSet<>();
set.add("apple");
set.add("banana");
set.add("apple"); // 중복이므로 무시됨

System.out.println(set); // [apple, banana]

• 순서가 없고, 중복을 허용하지 않음
• 구현체: HashSet, TreeSet, LinkedHashSet

7. Hashtable (해시테이블)

• Map의 오래된 구현체
• 멀티스레드 환경에서도 안전하게 작동 (동기화됨)
• 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블

Hashtable<String, Integer> table = new Hashtable<>();
table.put("apple", 1);
table.put("banana", 2);
System.out.println(table.get("banana")); // 2

• HashMap과 거의 비슷하지만 스레드 안전
• Null 키와 값 모두 허용하지 않음
• 오래된 클래스 → 보통은 HashMap + 동기화로 대체